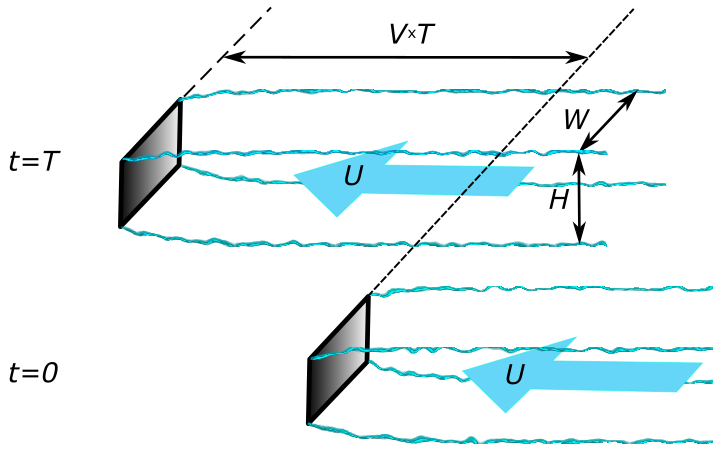
The width of the wake and the velocity in it are closely related to the drag of the mirror. In order to understand this it is convenient to change the frame of reference. Namely, instead of looking from the window of a moving car, we will now assume that we are standing still, while the car is passing by. In this frame of reference the air far ahead of the car is not moving. When the car is passing by it is leaving behind a wake, in which the air is moving. If, for simplicity, we will ignore the vertical component of the velocity, and will consider only the flow past the mirror, ignoring the car (well, does it look like not noticing an elephant in a china shop? No, not really), then what is happening can be illustrated in Fig.L6.
Over a time T the car, moving with the speed V, passes the distance VT. If the width and length of the wake are W and H, then in time T the volume of the wake has increased by VTWH. If the density of the air is ρ, the mass of the wake increases by ρVTWH. Let us denote U the velocity of the air inside the wake. Since the air inside the wake is moving, it has a kinetic energy, which is half of the product of the mass and the velocity squared. This means that over the time T the kinetic energy of the wake has increased by ρVTWHU2/2. Energy is conserved. Where did this energy came from? It came from the mirror. The mirror experiences a drag force, and therefore, according to the third Newton law, it exerts the equal and opposite force on the air. This force, D, does work, the magnitude of which is the product of the force and the distance, DVT. Equating this to the kinetic energy added and solving gives
DVT= ρVTWHU2/2
from which
D = ρWHU2/2.
Note how T cancels out. This is correct, as the drag force should not depend on T.